Tout mécanisme en mouvement ou fixe, formé par un ensemble de pièces a pour but de réaliser une ou plusieurs fonctions à travers les mouvement et les liaisons entre les différentes pièces qui le constituent.
La compréhension et l’étude des mécanismes passe par leur modélisation, afin de pouvoir mener à bien :
les mouvements des différentes pièces : c’est la cinématique
les efforts transmis et supportés par les différentes pièces ainsi que les « petites » déformations c’est la statique
interactions entre les efforts en jeu et les mouvements c’est la dynamique.
Les mobilités entre les différents composants d’un mécanismes seront modélisés graphiquement, de façon à construire un schéma cinématique qui a pour ambition de décrire l’ensemble des mouvements relatifs entre plusieurs groupes de pièces. Nous serons amenés à formuler quelques hypothèses :
les solides seront supposés indéformables
la géométrie des contacts sera supposée parfaite
Notion de degré de liberté
Il existe deux types de mouvement dans l’espace, la rotation et la translation. Tout autre mouvement est une combinaison de ces deux mouvements. Une rotation est toujours caractérisée par un axe ou un centre instantané et une translation est caractérisée par une direction instantanée selon un axe donné.
Dans l’espace à trois dimensions les directions sont représentées par un repère orthonormé direct. Ce repère possède trois axes Ox, Oy et Oz et un centre O.
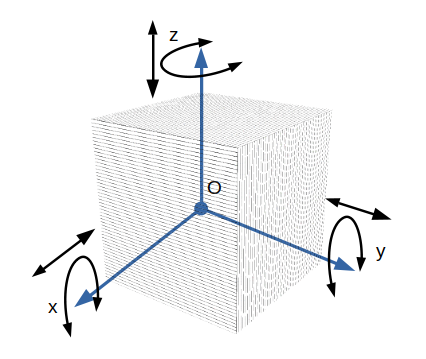
Chaque axe supporte deux mouvements élémentaires indépendants : une translation et une rotation. Chaque mouvement élémentaire constitue un degré de liberté. Le degré de liberté est donc le mouvement élémentaire que peut faire un objet selon un axe donné de l’espace. Puisque l’espace possède 3 axes donc chaque objet libre dans l’espace peut faire 2x3=6 mouvements indépendants donc 6 degrés de libertés.
Classes d’équivalence
Les pièces qui sont encastrées l’une par rapport à l’autre et qui n’ont aucun mouvement relatif possible seront regroupées dans un ensemble appelé «classe d’équivalence ». Du point de vue cinématique, il faut considérer alors ces pièces comme étant un seul et même solide. Dans un dessin d’ensemble, ces classes d’équivalence seront identifiées par des couleurs spécifiques.
Exemple : outil de découpe flan :
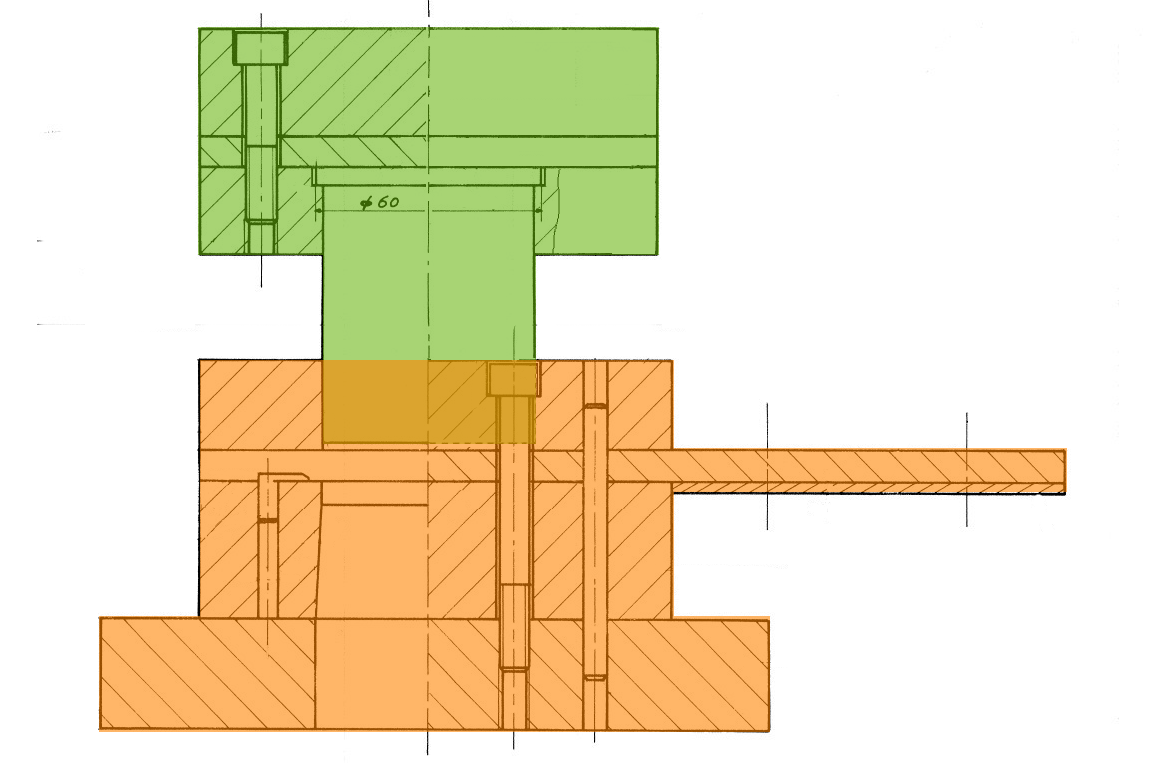
La partie supérieure « A » en vert (poinçon et les pièces associées ) représente une classe d’équivalence et la partie inférieure « B » en orangé (matrice et les pièces associées) représente une deuxième classe d’équivalence.
Graphe des liaisons
Parmi les classes d’équivalence identifiées, certaines sont en contact entre-elles. Il est alors possible de définir un «graphe des liaisons » qui permettra d’identifier les classes d’équivalence pour lesquelles une liaison mécanique existe. Ce graphe relie entre-elles les classes d’équivalence en contact.
ou bien
Géométrie du contact
Un contact entre deux pièces mécaniques ou classes d’équivalence (ensembles de pièces qui constituent un sous-système rigide) est caractérisé par sa nature géométrique. Le contact peut être sous plusieurs formes à savoir :
d’un point de contact
d’une ligne de contact (rectiligne ou non)
d’une surface de contact (plane ou non)
Chaque liaison ou contact entre deux pièces est caractérisé cinématiquement par les 6 mobilités relatives possibles : 3 rotations et 3 translations.
Les trois formes de base à partir desquelles l’ensemble des liaisons sera construit sont :
le plan
le cylindre
la sphère
Remarques :
1- La liaison est une modélisation théorique pour simplifier le calcul des problèmes mécaniques.
2- Toutes les liaisons sont repérées par une repère orthonormé direct dont l’origine est le centre de liaison et l’axe principal de la liaison est généralement confondu avec l’axe x.
Liaisons élémentaires
Il existe 6 liaisons simples, dites élémentaires, qui résultent de la combinaison des possibilités des contacts entre les 3 formes de bases citées plus haut :
Plan | Cylindre | Sphère | |
Sphère |
|
|
|
Cylindre |
|
| |
Plan |
|
Ce qui nous amène à définir les modèles des liaisons mécaniques élémentaires suivants :
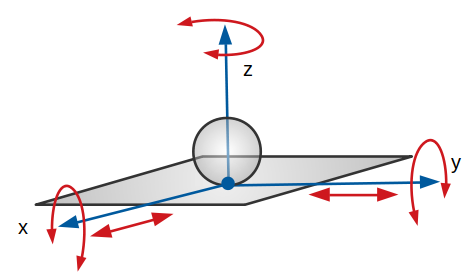
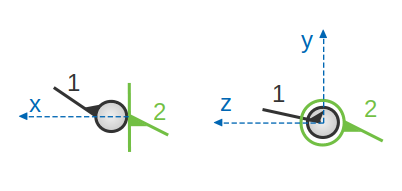
Liaison sphère-plan ou ponctuelle :
Cette liaison est théoriquement maintenue par un point qui est l’intersection de la sphère maintenue tangente au plan, quel que soit le sens de l’effort mécanique. Pour cela, cette liaison est appelée aussi liaison ponctuelle. La sphère peut se déplacer sur le plan, avec ou sans glissement, tout en gardant un contact permanent.
Le centre de la liaison est le point de contact et l’axe principal Ox.
Actions mécaniques transmissibles | Mouvements relatifs | ||||||||
Axes | Forces | Moments | Translations | Rotations | |||||
x | Fx | 0 | Mx | 0 | Tx | ≠0 | Rx | ≠0 | |
y | Fy | 0 | My | 0 | Ty | ≠0 | Ry | ≠0 | |
z | Fz | ≠0 | Mz | 0 | Tz | 0 | Rz | ≠0 | |
Nombre de degrés de libertés : 5 | |||||||||
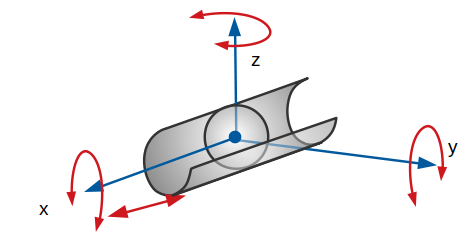
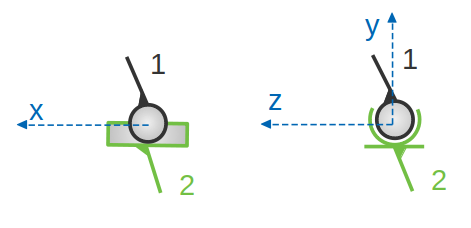
Liaison linaire annulaire :
Cette liaison est théoriquement maintenue par un arc de cercle qui est l’intersection de la sphère et du cylindre. La sphère est englobée par le cylindre. La sphère peut se déplacer et rouler dans le cylindre ou demi cylindre, avec ou sans glissement, tout en gardant un contact permanent.
Actions mécaniques transmissibles | Mouvements relatifs | ||||||||
Axes | Forces | Moments | Translations | Rotations | |||||
x | Fx | 0 | Mx | 0 | Tx | ≠0 | Rx | ≠0 | |
y | Fy | ≠0 | My | 0 | Ty | 0 | Ry | ≠0 | |
z | Fz | ≠0 | Mz | 0 | Tz | 0 | Rz | ≠0 | |
Nombre de degrés de libertés : 4 | |||||||||
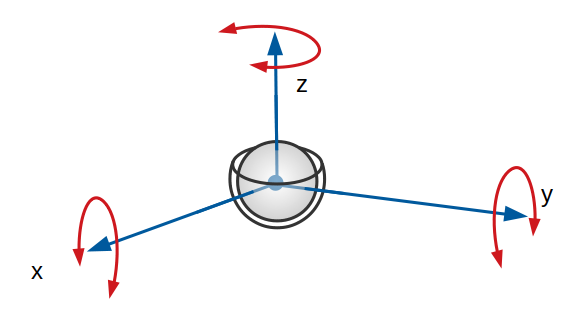
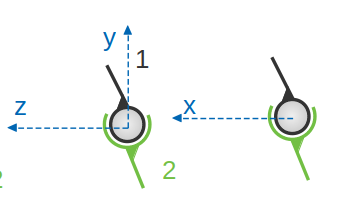
Liaison Rotule ou Sphérique
Cette liaison est théoriquement maintenue par une surface sphérique qui est l’intersection de la sphère intérieure et de la sphère extérieure. Une sphère est englobée par une autre sphère. La sphère intérieure peut tourner dans la sphère extérieure (ou partie de sphère) suivant 3 directions, tout en gardant un contact permanent.
Actions mécaniques transmissibles | Mouvements relatifs | ||||||||
Axes | Forces | Moments | Translations | Rotations | |||||
x | Fx | ≠0 | Mx | 0 | Tx | 0 | Rx | ≠0 | |
y | Fy | ≠0 | My | 0 | Ty | 0 | Ry | ≠0 | |
z | Fz | ≠0 | Mz | 0 | Tz | 0 | Rz | ≠0 | |
Nombre de degrés de libertés : 3 | |||||||||
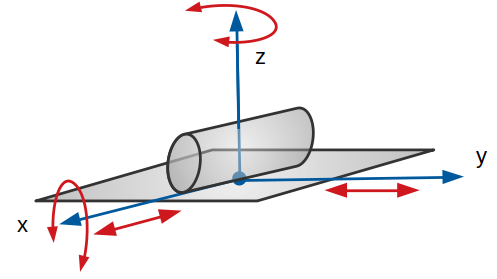
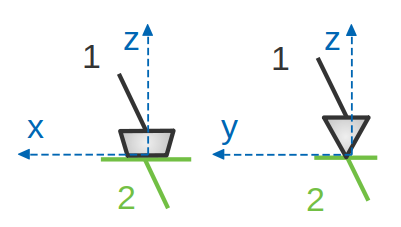
Linéaire rectiligne
Cette liaison est théoriquement maintenue par une ligne droite qui est l’intersection du cylindre et du plan tangent extérieur. Le cylindre peut tourner sur le plan suivant 2 directions et peut se déplacer aussi selon deux directions, tout en gardant un contact permanent.
Actions mécaniques transmissibles | Mouvements relatifs | ||||||||
Axes | Forces | Moments | Translations | Rotations | |||||
x | Fx | 0 | Mx | 0 | Tx | ≠0 | Rx | ≠0 | |
y | Fy | 0 | My | ≠0 | Ty | ≠0 | Ry | 0 | |
z | Fz | ≠0 | Mz | 0 | Tz | 0 | Rz | ≠0 | |
Nombre de degrés de libertés : 4 | |||||||||
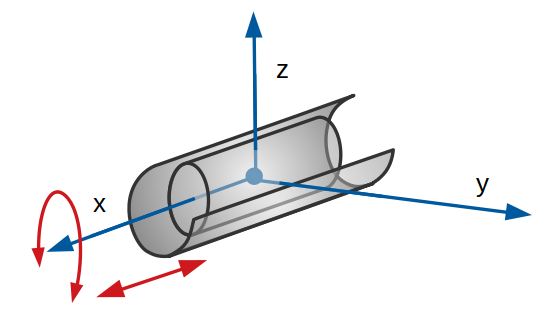
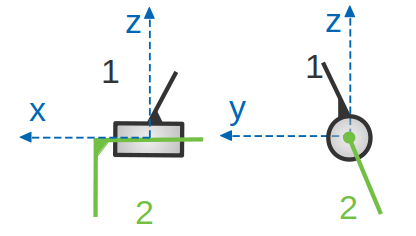
Pivot glissant
Cette liaison est théoriquement maintenue par une surface cylindrique qui est l’intersection du cylindre intérieure et du cylindre extérieur. Un cylindre est entouré par un autre cylindre. Le cylindre intérieur peut tourner dans le cylindre extérieur (ou une partie de cylindre) suivant 1 seule direction et peut translater aussi suivant une seule direction, tout en gardant un contact permanent.
Actions mécaniques transmissibles
Mouvements relatifs
Axes
Forces
Moments
Translations
Rotations
x
Fx
0
Mx
0
Tx
≠0
Rx
≠0
y
Fy
≠0
My
≠0
Ty
0
Ry
0
z
Fz
≠0
Mz
≠0
Tz
0
Rz
0
Nombre de degrés de libertés : 2
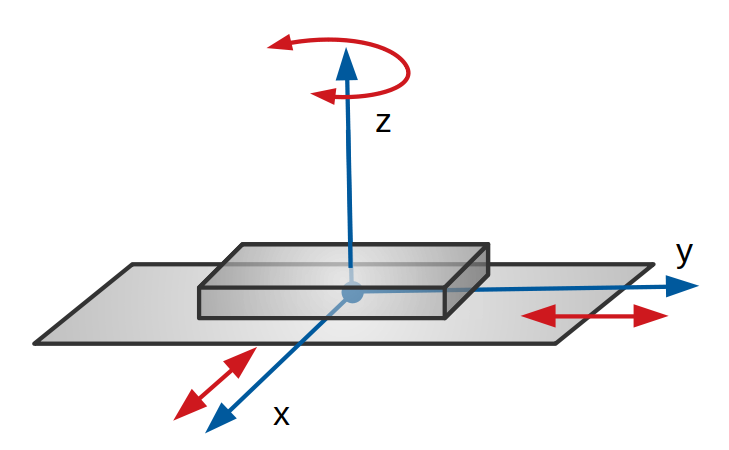
Appui plan
Cette liaison est théoriquement maintenue par un plan qui est l’intersection des deux solides en contact. Le plan peut tourner sur l’autre plan suivant une seule direction et peut se déplacer aussi selon deux directions, tout en gardant un contact permanent.
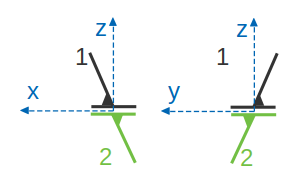
Actions mécaniques transmissibles
Mouvements relatifs
Axes
Forces
Moments
Translations
Rotations
x
Fx
0
Mx
≠0
Tx
≠0
Rx
0
y
Fy
0
My
≠0
Ty
≠0
Ry
0
z
Fz
≠0
Mz
0
Tz
0
Rz
≠0
Nombre de degrés de libertés : 3
Liaisons composées
L’association de deux liaisons élémentaires permet de construire d’autres liaisons, appelées liaisons composées. Elles seront définies par deux surfaces de contact, et donneront lieu à des libertés de mouvements spécifiques.
Exemple de liaisons composées :
Il existe souvent plusieurs combinaisons possibles pour une même liaison composée.
Liaison encastrement :
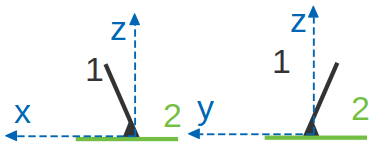
Cette liaison est théoriquement maintenue par encastrement. Les deux pièces constituent une classe d’équivalence. La pièce ne peut faire aucune rotation(s) et ne peut faire aucune translation. Le contact est toujours permanent.
Actions mécaniques transmissibles
Mouvements relatifs
Axes
Forces
Moments
Translations
Rotations
x
Fx
0
Mx
≠0
Tx
≠0
Rx
0
y
Fy
0
My
≠0
Ty
≠0
Ry
0
z
Fz
≠0
Mz
0
Tz
0
Rz
≠0
Nombre de degrés de libertés : 3
Sphérique à doigt
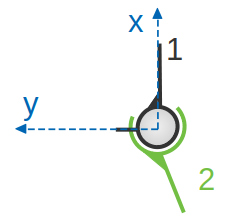
Cette liaison est théoriquement maintenue par un globe de sphère qui est l’intersection de 1 et 2 et un contact ponctuel par le doit de 1, dans une rainure de 2, pour empêcher la rotation selon X. Une sphère est englobée par une autre sphère avec blocage. La sphère intérieure peut tourner dans la sphère extérieure autour de l’axe Y et Z. Le doigt a pour rôle de bloquer la rotation autour de l’axe X. La pièce ne peut faire que deux rotations et ne peut faire aucune translation(s), tout en gardant un contact permanent. L’axe principal de liaison est Z.
Actions mécaniques transmissibles
Mouvements relatifs
Axes
Forces
Moments
Translations
Rotations
x
Fx
0
Mx
≠0
Tx
≠0
Rx
0
y
Fy
0
My
≠0
Ty
≠0
Ry
0
z
Fz
≠0
Mz
0
Tz
0
Rz
≠0
Nombre de degrés de libertés : 3
Liaison pivot
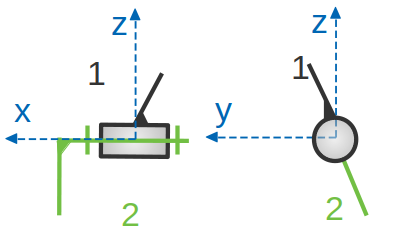
Cette liaison est théoriquement maintenue par un cylindre et deux plans. Un cylindre est entouré par un autre cylindre et les plans latéraux pour bloquer la translation selon l’axe X. La pièce 1 ne peut faire qu’une seule rotation autour de l’axe X. L’axe principal de liaison est X
Actions mécaniques transmissibles
Mouvements relatifs
Axes
Forces
Moments
Translations
Rotations
x
Fx
≠0
Mx
0
Tx
0
Rx
≠0
y
Fy
≠0
My
≠0
Ty
0
Ry
0
z
Fz
≠0
Mz
≠0
Tz
0
Rz
0
Nombre de degrés de libertés : 1
Liaison glissière
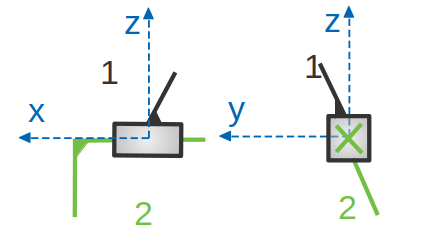
Cette liaison est théoriquement maintenue par deux plans perpendiculaires qui forment le contact entre les deux pièces. Cette liaison permet que une seule translation et aucune rotation. L’axe principal de liaison est X.
Actions mécaniques transmissibles
Mouvements relatifs
Axes
Forces
Moments
Translations
Rotations
x
Fx
0
Mx
≠0
Tx
≠0
Rx
0
y
Fy
≠0
My
≠0
Ty
0
Ry
0
z
Fz
≠0
Mz
≠0
Tz
0
Rz
0
Nombre de degrés de libertés : 1
 Mon catalogue
Mon catalogue 

































 22478
22478  ConcepTEK.net
ConcepTEK.net 