Mon catalogue 
Le terme « fiabilité » ou " fiabilité des systèmes" est une notion introduite dans les années 60 pour traduire le terme anglo-saxon « reliability ». La fiabilité est la science des défaillances. On veut dire par système tout ensemble de composants ou pièces liés ensemble pour réaliser une fonction ou répendre à un besoin fonctionnel.
Définitions de la fiabilité
C’est l’aptitude d’un dispositif 'S' à accomplir une fonction requise, dans des conditions données, pendant une durée donnée. Le terme fiabilité représente une probabilité de succès ou un pourcentage de succès.
L’expression mathématique de la fiabilité est :
= probabilité (S non défaillant sur [0, t])
est une fonction non croissante variant de 1à 0 sur
La fiabilité n’est pas la seule probabilité intéressante liée au fonctionnement d’un système, on trouve également le deux probabilités suivantes :
PUB :Nos recommandations d'articles en soldes :
LIHAOPING 45 Résistant SB SD SDX C12-10-110 C16-16-100 Chanfreinage Outils CNC Tour Fraise Support Endmill éventuelles MW09 SCstuff éventuelles MG;
🔗Cliquer & Acheter: https://s.click.aliexpress.com/e/_EHCNKrx
La disponibilité 
représente la probabilité pour que le système S soit non défaillant à l’instant t. On remarquera que dans le cas de systèmes non réparables, la définition de la disponibilité est équivalente à celle de la fiabilité :
= probabilité (S non défaillant à l’instant t)
La maintenabilité 
représente le complément à 1 de la probabilité pour que le système ne soit pas réparé sur l’intervalle [0, t] sachant qu’il est défaillant à l’instant t=0.
Probabilité (S non réparé sur [0, t]).
Cette notion ne concerne que les systèmes réparables. 
est une fonction non décroissante variant de 0 à 1 sur , lorsque t tend vers l’infini, la fiabilité tend vers 0 et la maintenabilité vers 1
Signification de quelques signes
Un certain nombre de signes désignant des moyennes temporelles, Nous utiliserons les notations suivantes :
MTTF Durée moyenne de bon fonctionnement d’un système avant la première défaillance (Mean Time To Failure) ;
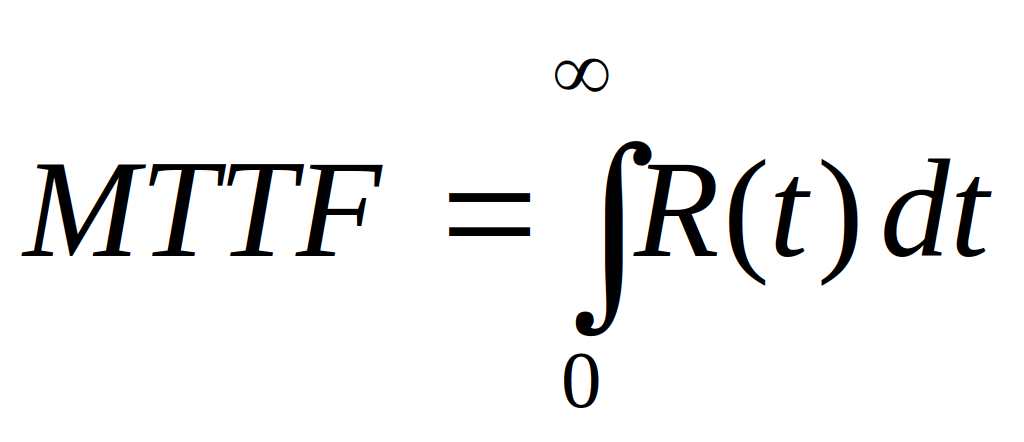
MTTR Durée moyenne des temps de réparation (Mean Time To Repair) ;
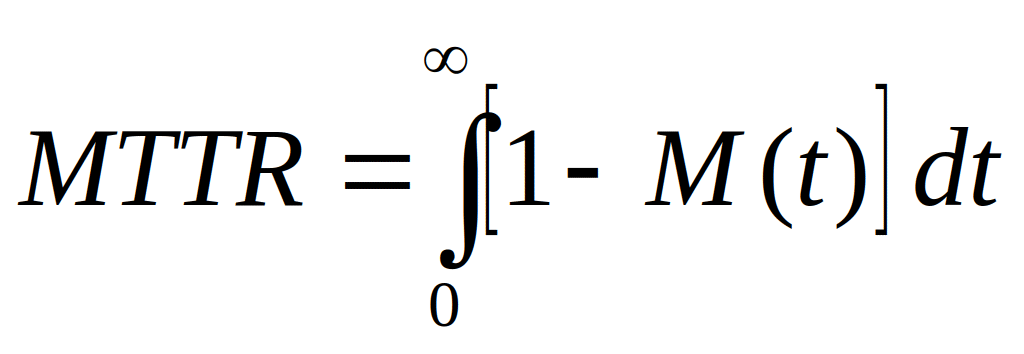
MUT Durée moyenne de bon fonctionnement après réparation (Mean Up Time)
MDT Durée moyenne de défaillance (Mean Down Time)
MTBF Moyenne des temps entre deux défaillances d’un système réparable (Mean Time Between Failure).
MTBF=MUT+MDT
Taux de défaillance instantanée
Taux de réparation instantanée
Relations fondamentales
Temps moyen de bon fonctionnement et temps moyen de réparation
Soit T la variable aléatoire mesurant la durée du temps de bon fonctionnement du système. La définition de la fiabilité s’écrit alors :
La fonction de répartition U de la variable aléatoire T s’écrit alors 
:
représente la probabilité de défaillance sur [0, t].
La densité de défaillance u (t), si elle existe vaut donc :
On en déduit alors le temps moyen de bon fonctionnement, s’il existe : 
d’où en intégrant par partie on trouve 
=
car
tend vers 0
Taux de défaillance instantané et taux de réparation instantané
On a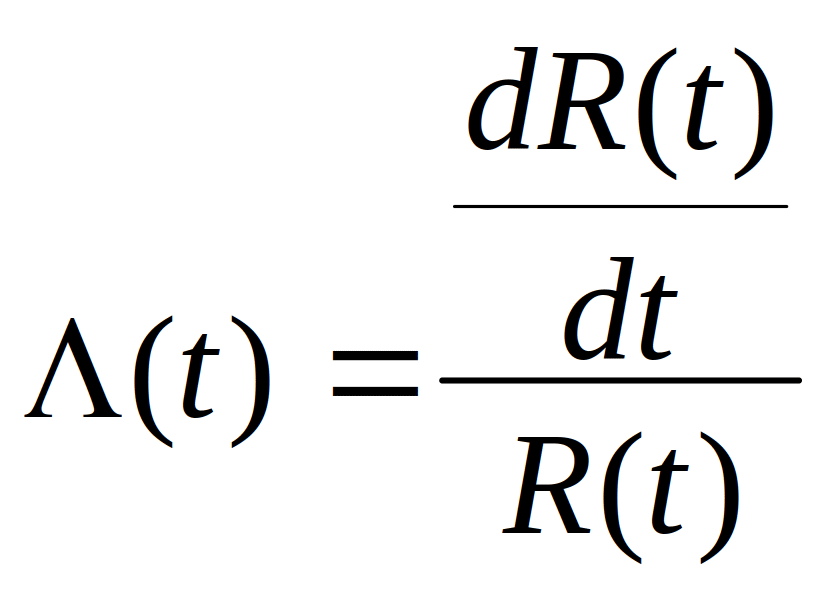 
et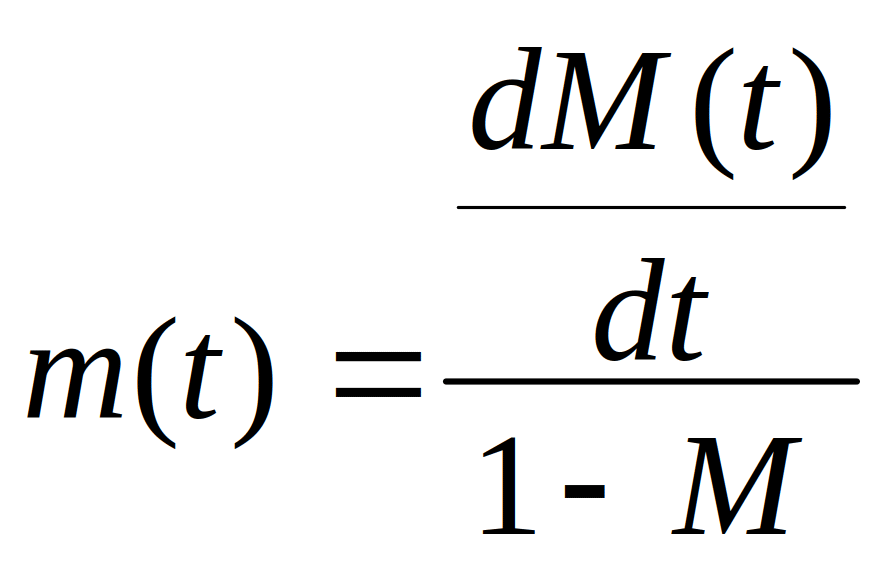 
; On déduit alors :
et 
.
La densité de probabilité u (t) s’écrit alors :
De la même manière, la densité de probabilité de réparation m (t) s’écrit : 
Représentation de la logique d’un système
Le premier problème rencontré par le technicien fiabiliste dans l’étude de la fiabilité d’un système est la description de ce système.
Considérerons un système formé de n éléments devant remplir une fonction donnée. Si chaque élément n’a qu’un nombre fini d’états, alors on aura les deux cas suivants :
L’élément est normalement en marche dans le système et il a deux états possibles : état de marche et état de panne ;
L’élément est normalement à l’arrêt dans le système et ne démarre qu’en secours d’un élément principal (élément en redondance passive). Il a alors quatre états possibles : en marche, en réparation, à l’arrêt en bon état, à l’arrêt en panne.
Le nombre d’états du système croit avec le nombre des éléments. En effet, si chaque élément admet 2 états, le système admet 2n états.
Un système est dit cohérent si :
Lorsque le système est en panne, aucune défaillance ne rétablit le bon état du système ;
Lorsque le système est en marche, aucune réparation n’induit la panne du système ;
La panne de tous les éléments induit la panne du système ;
La bonne marche de tous les éléments entraîne la bonne marche du système.
Définition Digramme de fiabilité
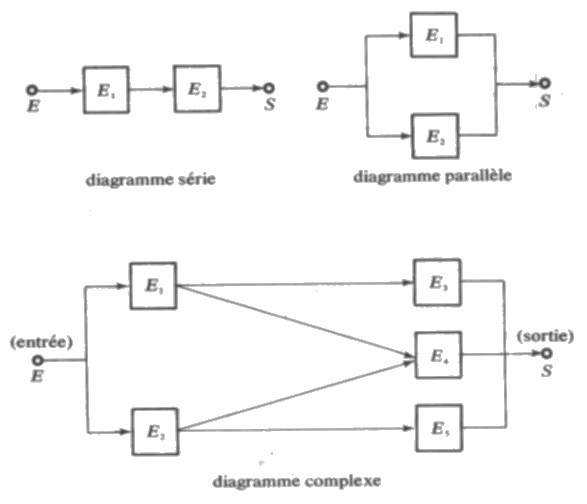
C’est la représentation la plus naturelle de la logique de fonctionnement d’un système car elle est souvent proche du schéma fonctionnel du système.
Le système fonctionne s’il existe un chemin de succès. La liste des chemins de succès permet donc de représenter l’ensemble des états de marche du système.
Dans l’exemple précédent, les chemins de succès sont :
E1E3, E1E4, E2E4, E2E5
Le diagramme logique de fiabilité peut représenter des cas plus complexes :
Les blocs du diagramme de fiabilité représentent éléments. Il est souvent intéressant de regrouper un certain nombre d’éléments pour constituer un seul bloc avec eux ; un tel bloc sera souvent appelé un macro- élément.
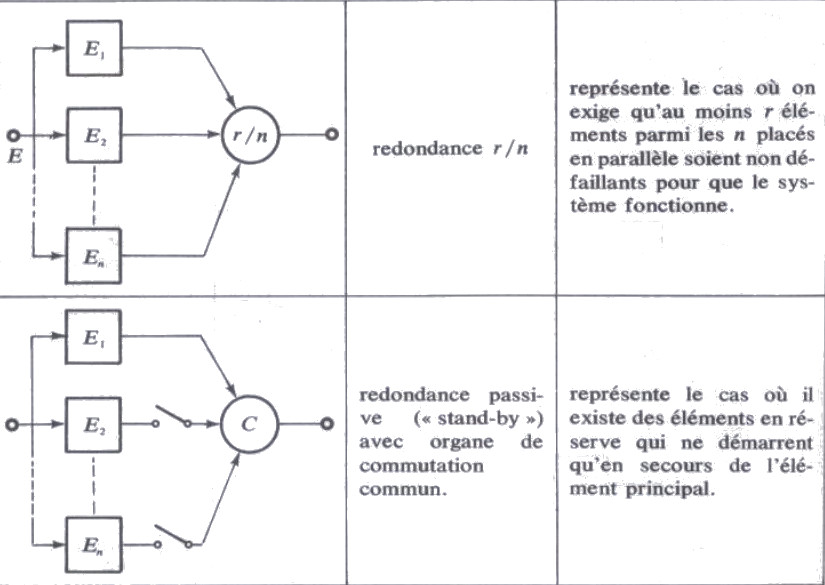
Symboles de redondance
31648 
ConcepTEK.net 
