On note {T}_O en fonction de ses éléments de réduction :

{T}_O =

2- Propriétés des torseurs :

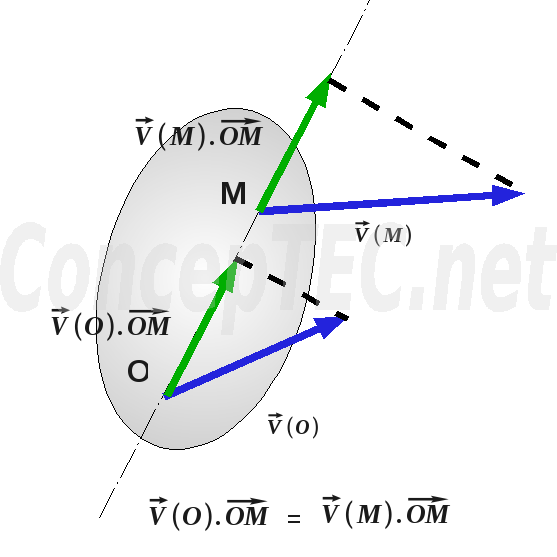
2.1 Équiprojectivité

En faisant le produit scalaire par , on obtient directement la relation d'équiprojectivité des moments aux points O et P c 'est à dire :

Nos recommandations d'articles en soldes :

LIHAOPING 45 Résistant SB SD SDX C12-10-110 C16-16-100 Chanfreinage Outils CNC Tour Fraise Support Endmill éventuelles MW09 SCstuff éventuelles MG;

🔗Cliquer & Acheter: https://s.click.aliexpress.com/e/_EHCNKrx

 Antisymétrie :

Soit un champ de vecteurs, c’est-à-dire une application de l’espace affine euclidien E³ (ou d’une partie de E³ ) dans l’espace vectoriel E3 :

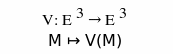
Le champ de vecteurs est antisymétrique si il existe un vecteur tel que :

Quels que soient  P et  M appartenant à   E ³ ,

On dit alors que le champ de vecteur est un torseur. Pour connaitre complètement un torseur, il suffit de connaitre sa résultante, c’est à dire son vecteur , et son moment en un point, c’est à dire sa valeur en un point P particulier.

Le couple constitue les éléments de réduction en P du torseur.

 3- Formule de transport des moments:

Pour un torseur {T}_O d'éléments de réduction au point O.

la résultante et le moment ;

Author: ConcepTEK.netEmail: Cette adresse e-mail est protégée contre les robots spammeurs. Vous devez activer le JavaScript pour la visualiser.

Autres publications

• Augmentez votre visibilité Web grace à notre Espace Professionnel (Hits 446)
• Pourquoi je crée mon catalogue sur ConcepTEK.net (Hits 460)
• Vous cherchez un fournisseur ? (Hits 940)
• Vous êtes un fournisseur ou industriel ? (Hits 1014)
• Le polycarbonate, un plastique exceptionnel, résistant et rigide (Hits 4117)