Soit un cylindre, de longueur « L », sous pression. On considère sa moitié isolée obtenue par une coupe fictive par un plan passant par l'axe de révolution est représenté par la figure suivante :

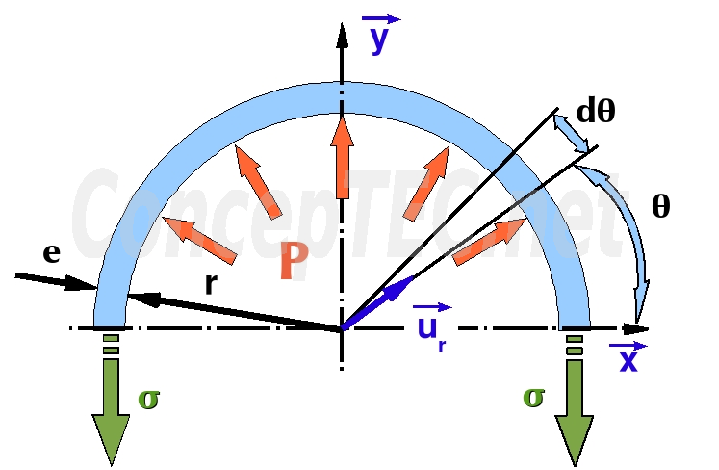
Cette figure montre aussi les contraintes σ dans une section longitudinale.

la pression "P" est supposée constante sur toute la paroi.

L'épaisseur de la paroi est notée par "e"

Nos recommandations d'articles en soldes :

LIHAOPING 45 Résistant SB SD SDX C12-10-110 C16-16-100 Chanfreinage Outils CNC Tour Fraise Support Endmill éventuelles MW09 SCstuff éventuelles MG;

🔗Cliquer & Acheter: https://s.click.aliexpress.com/e/_EHCNKrx

le rayon interne est noté "r"

 Lorsqu'on isole le demi cylindre, et on le considère en équilibre, alors le PFS donne

Or les forces appliquées au demi cylindre sont :

• La forces exercée par l'autre moitié est décrite par :

avec S la section de paroi ;

S = e.L

• et la somme des forces due à la pression P exercé par le fluide sur l'élément de surface dS_p qui peut être décrite par

  

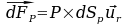
  or

  

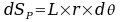
La pression P est appliquées perpendiculairement à la paroi selon . Cette paroi est circulaire et symétrique par rapport à l'axe ; donc les composantes selon l'axe vont s'annuler symétriquement.

Ce ci peut se traduire mathématiquement par l'équation suivante :

or

Or la fonction « cos » est symétrique donc son intégrale entre 0 et π est nulle.

Donc on peut écrire

donc

Finalement

(1)

Condition de résistance :

avec « R_pe » la limite pratique à l'élasticité

« R_e »est la limite d'élasticité

« s » est un coefficient de sécurité qui dépend de l'application de la pièce.

Calcul de la déformation :

L'élément de longueur « dl » du périmètre du cercle est

cet élément de longueur subit une contrainte due à la pression.

Or on sait d'après le calcul en traction que

E : module d"élasticité

soit l'allongement que subit

donc

donc

comme d'après (1)

donc

donc l'allongement du périmètre est

Finalement

la déformation du périmètre est

Author: ConcepTEK.netEmail: Cette adresse e-mail est protégée contre les robots spammeurs. Vous devez activer le JavaScript pour la visualiser.

Autres publications

• Augmentez votre visibilité Web grace à notre Espace Professionnel (Hits 569)
• Pourquoi je crée mon catalogue sur ConcepTEK.net (Hits 576)
• Vous cherchez un fournisseur ? (Hits 1155)
• Vous êtes un fournisseur ou industriel ? (Hits 1261)
• Le polycarbonate, un plastique exceptionnel, résistant et rigide (Hits 4370)