--------------------------------------

1. Principe de l'essai de traction :

L’essai consiste à soumettre une éprouvette à un effort de traction, et cela, généralement jusqu’à rupture en vue de déterminer une ou plusieurs caractéristiques mécaniques.

On impose en général une déformation croissante à une éprouvette sur laquelle on trace deux repères initialement distincts de L₀, et on mesure simultanément l’effort F et l’allongement :

ΔL = L - L₀.

---

---

2. Forme et dimensions de l'éprouvette de l'essai de traction

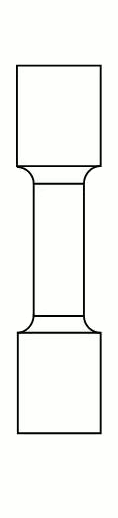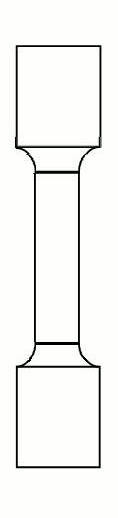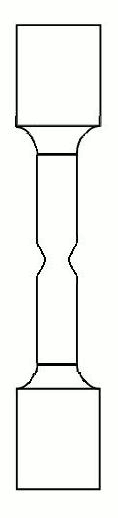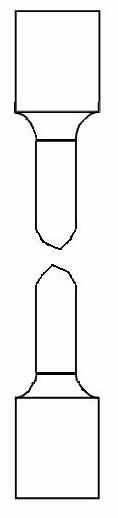
L’éprouvette est généralement obtenue par usinage d’un prélèvement d’un produit ou d’une ébauche moulée. Sa section est habituellement plate (fig. 1 (1)) ou circulaire(fig. (2)).

---

---

 

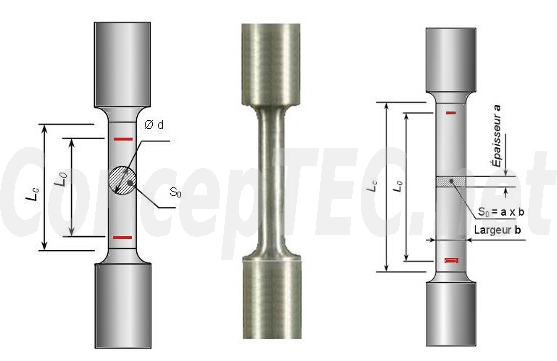
Éprouvette cylindrique et éprouvette plate

Fig. 1 : géométrie des éprouvettes de traction.

 

Toute éprouvette doit comporter une partie calibrée de longueur L₀ qui doit être usinée d’une manière très soignée avec des tolérances bien définies. Cette longueur doit être proportionnelle à la section selon l’expression empirique :

avec S₀ : section initiale de la partie calibrée, k = 5.65

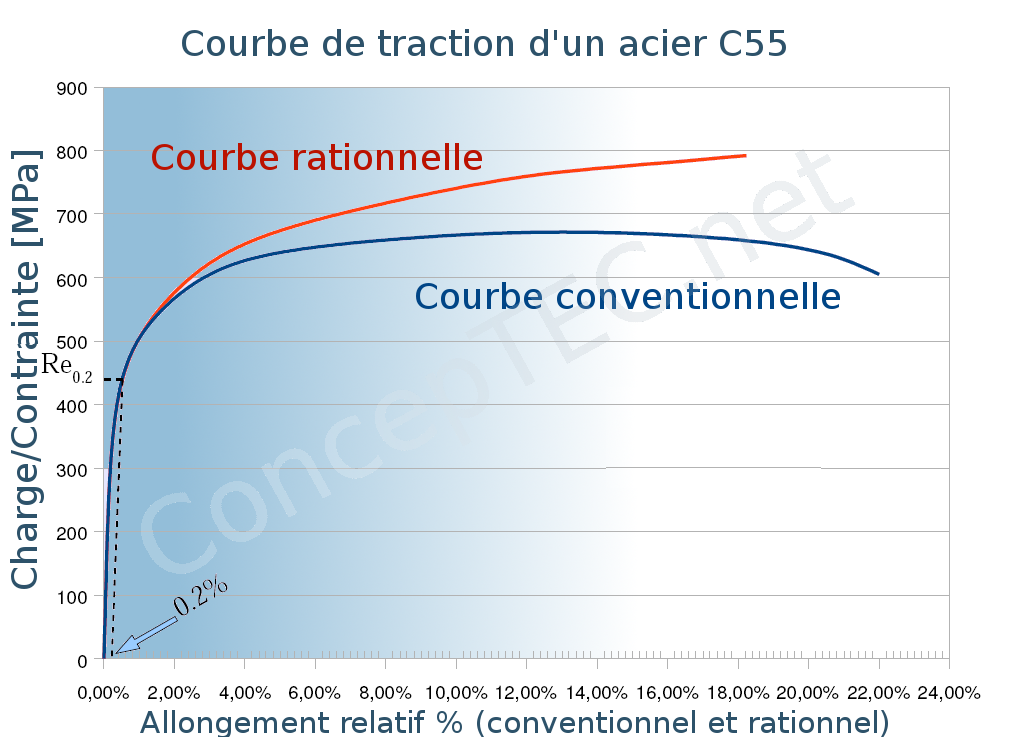
Diagramme conventionnel de traction

Forme classique d’un diagramme de traction :

Le diagramme de traction représente l’évolution de la charge unitaire

en fonction du taux d’allongement

La courbe conventionnelle a l'allure donnée par la figure suivante :

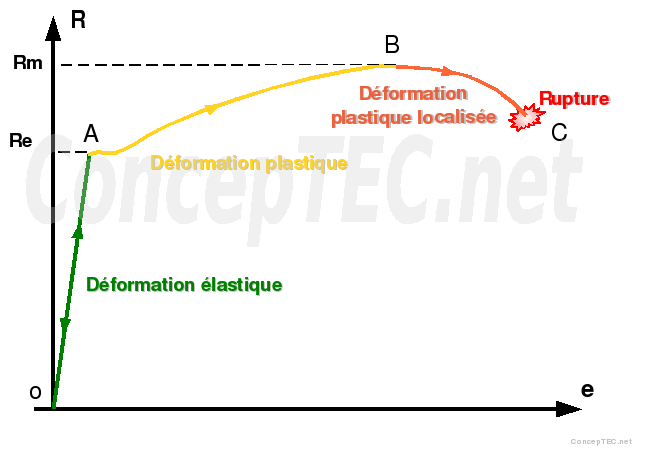
Fig. 2: Allure de la courbe conventionnelle de traction

 

Cette courbe contient diverses régions :

• OA : domaine élastique à déformation réversible R=E.e (le coefficient de proportionnalité est le module d’Young E); le point A marque la limite du domaine élastique ;

• AB : domaine de déformation permanente homogène ou de déformation plastique répartie ; le point B se situe à charge maximale et au début de la striction ;

• BC : domaine de striction ou de déformation plastique localisée ; C : point de rupture de l’éprouvette.

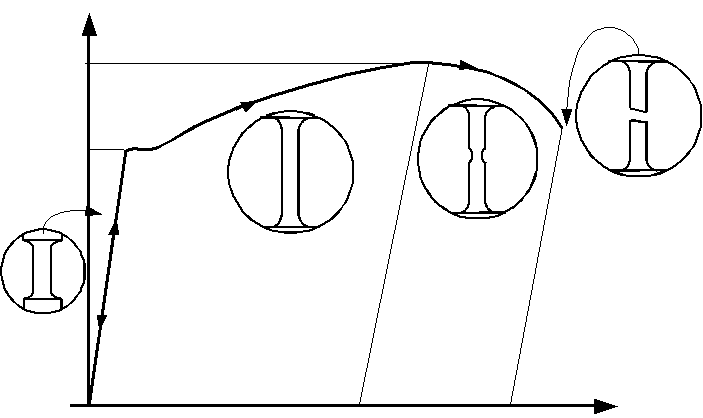
Fig. 3 représentations des éprouvettes selon la charge appliquée

 

Propriétés "classiques" déduites de l’essai de traction

Limite apparente d’élasticité

en MPa ; F en N ; S₀ en mm²

Certaines courbes de traction ne présentent pas de limite apparente d’élasticité nette (aciers austénitiques, aluminium, ...), de telle sorte que l’on définit une limite conventionnelle d’élasticité (souvent fixée à 0. 1% ou 0.2%).

en Mpa

 

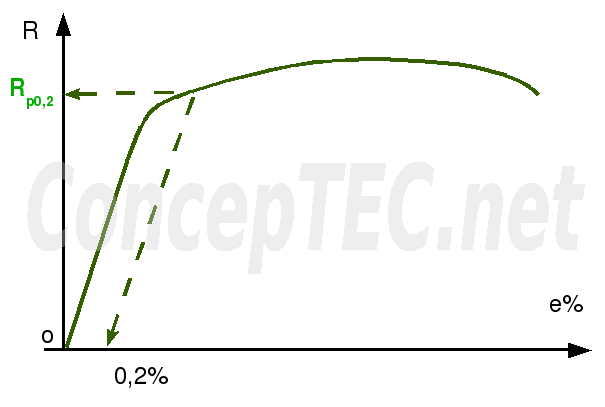
Fig.4 Limite conventionnelle d’élasticité

 Transition élasto–plastique :

Dans certains cas (aciers ferritiques), la transition élastique - plastique se fait de façon hétérogène (bande de Piobert Lüders). Dans ce cas, la courbe possèdera un crochet de traction suivi d’un palier de charge. La norme définit trois éléments :

- une limite supérieure d’élasticité R_eH en (MPa);

- une limite inférieure d’élasticité R_el en (MPa);

- la longueur du palier A_p en (%).

 

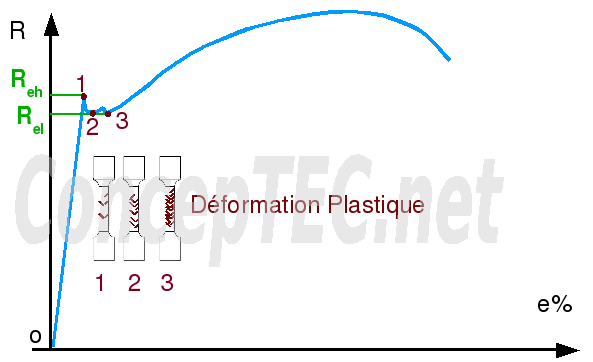
Fig. 5: Limite inférieure et supérieure d’écoulement ( palier de Piobert Lüders)

 

 Résistance à la traction

Défini par

Avec F_m= charge maximale; Rm en (MPa).

Allongement pour cent après rupture

Défini par A%=

Ou L_u = longueur de l’éprouvette reconstituée après rupture.

Striction

On définit

- le coefficient de striction :

- l’allongement de striction

Où S_u est la section minimale de l’éprouvette après rupture.

Digramme rationnel de traction

C'est quoi le diagramme rationnel

 La courbe conventionnelle permet de définir des propriétés mécaniques permettant de caractériser un matériau, mais elle ne peut pas renseigner pas sur la loi de comportement (relation entre la charge réelle et la déformation réelle) dans les domaines élastique et plastique du matériau car elle ne teint pas compte de la diminution de la section.

 

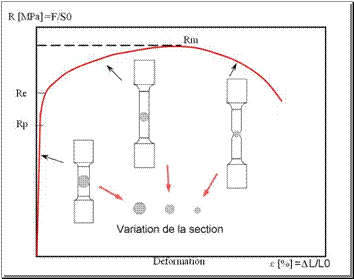
Fig. 6: Variation de la section au cours de l’essai

 

La courbe rationnelle (ou le diagramme rationnel) de traction est la représentation de la courbe en ordonnées la contrainte vraie, et en abscisses la déformation rationnelle.

Contrainte vraie :

Elle tient compte de la variation de section au cours de l’essai (Fig.5) et est égale à la charge F rapportée à la section instantanée S

En admettant que le volume de la partie calibrée de l’éprouvette reste constant, on a:

S₀L₀ = SL = S(L₀+ΔL)

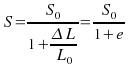
D'ou σ = F/S = F/S₀ (1+e) = R (1+e)

σ = R (1+e)

Déformation rationnelle

Soit ΔL l’allongement de la poutre depuis le début de l’essai jusqu’à un instant t de l’essai (avant la rupture).

Donc ΔL =L-L₀

De plus, la quantité ΔL/L₀ à un instant donné de l’essai ne correspond pas à la véritable déformation, qui par définition vaut ΔL/L avec L variable continûment au cours de l’essai.

Soit dL l’allongement instantané lorsque la longueur de la poutre est L (>L₀)

d L = L( t + t_e ) - L ( t )

t+t_e est un instant juste après t (t_e est un temps infiniment petit)

et on a l’allongement depuis le début de l’essai est Δ L, en considérant des taux allongements infiniment petits :

Alors le taux d’allongement rationnel (réel) depuis t = 0 (longueur = L₀) jusqu’à l’instant t > 0 (longueur = L) s'écrit mathématiquement

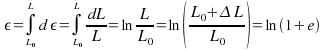
donc ε = ln (1+e)

La courbe qui représente (σ, ε) est appelée « Le diagramme rationnel de traction ». Il se déduit du diagramme conventionnel.